Kalkulus (calculus) adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret takterhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana geometri adalah ilmu mengenai bentuk dan aljabar adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.
Kalkulus memiliki dua cabang utama, kalkulus diferensial dan kalkulus integral yang saling berhubungan melalui teorema dasar kalkulus. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematika lainnya yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematika.
1. sistem bilangan riil
Bilangan riil atau bilangan real menyatakan bilangan yang bisa dituliskan dalam bentuk desimal, seperti 2,4871773339… atau 3.25678. Bilangan real meliputi bilangan rasional, seperti 42 dan −23/129, dan bilangan irasional, seperti π dan sqrt2. Bilangan rasional direpresentasikan dalam bentuk desimal berakhir, sedangkan bilangan irasional memiliki representasi desimal tidak berakhir namun berulang. Bilangan riil juga dapat direpresentasikan sebagai salah satu titik dalam garis bilangan. Definisi popular dari bilangan real meliputi klas ekivalen dari deret Cauchy rasional, irisan Dedekind, dan deret Archimides. Bilangan riil ini berbeda dengan bilangan kompleks yang termasuk di dalamnya adalah bilangan imajiner.
Aksioma (postulat) medan
Bilangan riil, beserta operasi penjumlahan dan perkalian, memenuhi postulat berikut. Misalkan x,y dan z merupakan anggota himpunan bilangan riil R, dan operasi x+y merupakan penjumlahan, serta xy merupakan perkalian. Maka:
2. Pertidaksamaan
Pendahuluan
1. sistem bilangan riil
Bilangan riil atau bilangan real menyatakan bilangan yang bisa dituliskan dalam bentuk desimal, seperti 2,4871773339… atau 3.25678. Bilangan real meliputi bilangan rasional, seperti 42 dan −23/129, dan bilangan irasional, seperti π dan sqrt2. Bilangan rasional direpresentasikan dalam bentuk desimal berakhir, sedangkan bilangan irasional memiliki representasi desimal tidak berakhir namun berulang. Bilangan riil juga dapat direpresentasikan sebagai salah satu titik dalam garis bilangan. Definisi popular dari bilangan real meliputi klas ekivalen dari deret Cauchy rasional, irisan Dedekind, dan deret Archimides. Bilangan riil ini berbeda dengan bilangan kompleks yang termasuk di dalamnya adalah bilangan imajiner.
Aksioma (postulat) medan
Bilangan riil, beserta operasi penjumlahan dan perkalian, memenuhi postulat berikut. Misalkan x,y dan z merupakan anggota himpunan bilangan riil R, dan operasi x+y merupakan penjumlahan, serta xy merupakan perkalian. Maka:
- Aksioma 1 (hukum komutatif): x+y = y+x, dan xy = yx
- Aksioma 2 (hukum asosiatif): x+(y+z) = (x+y)+z dan x(yz) = (xy)z
- Aksioma 3 (hukum distributif): x(y+z) = (xy + xz)
- Aksioma 4: Eksistensi unsur identitas. Terdapat dua bilangan riil berbeda, yang dilambangkan sebagai 0 dan 1, sehingga untuk setiap bilangan riil x kita mendapatkan 0+x=x dan 1.x=x.
- Aksioma 5: Eksistensi negatif, atau invers terhadap penjumlahan. Untuk setiap bilangan riil x, terdapat bilangan riil y sehingga x+y=0. Kita dapat juga melambangkan y sebagai -x.
- Aksioma 6: Eksistensi resiprokal, atau invers terhadap perkalian. Untuk setiap bilangan riil x tidak sama dengan 0, terdapat bilangan riil y sehingga xy=1. Kita dapat melambangkan y sebagai 1/x.
Aksioma (postulat) urutan
Kita akan mengasumsikan terdapat himpunan R+, yang disebut sebagai bilangan positif yang merupakan himpunan bagian dari R. Misalkan juga x dan y adalah anggota R+. Himpunan bagian ini memenuhi aksioma urutan berikut ini:- Aksioma 7: x+y dan xy merupakan anggota R+
- Aksioma 8: Untuk setiap x yang tidak sama dengan 0, x anggota R+ atau -x anggota R+, tapi tidak mungkin keduanya sekaligus
- Aksioma 9: 0 bukan anggota R+.
Aksioma (postulat) kelengkapan
- Aksioma 10: Setiap himpunan bilangan riil S yang memiliki batas atas memiliki supremum, yakni ada suatu bilangan riil B sehingga B=sup(S).
2. Pertidaksamaan
Kalimat/pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih. Dua notasi dasar dalam pertidaksamaan adalah:
3. Nilai Mutlak
Beberapa sifat-sifat nilai mutlak adalah sebagai berikut ini :
Jika ɑ, b ∈R, maka :
| ɑ |≥ 0;
|- ɑ |=| ɑ |
√ɑ2 = | ɑ |;
| ɑ | < b
jika dan hanya jika dimana b > 0
| ɑ | > b jika dan hanya jika ɑ < -b atau ɑ > b
| ɑ ± b |= |b ± ɑ |;
| ɑb |= | ɑ || b |;
| ɑ/b |=| ɑ |/| b |, b ≠0;
|(ɑ+ b) | ≥ | ɑ |-| b |;
|(ɑ- b) | ≥ | ɑ |-| b |;
|(ɑ- b) | ≤ | ɑ |+| b |;
- Notasi < menyatakan lebih kecil, contohnya: 2<3 dan x + 1 < 3.
- Notasi > menyatakan lebih besar, contohnya: 3>2 dan 3x + 1 > 5.
3. Nilai Mutlak
Harga mutlak disimbolkan dengan garis vertikal sebagai tanda kurungnya. Misalnya nilai mutlak dari ɑ dituliskan | ɑ |
Beberapa sifat-sifat nilai mutlak adalah sebagai berikut ini :
Jika ɑ, b ∈R, maka :
| ɑ |≥ 0;
|- ɑ |=| ɑ |
√ɑ2 = | ɑ |;
| ɑ | < b
jika dan hanya jika dimana b > 0
| ɑ | > b jika dan hanya jika ɑ < -b atau ɑ > b
| ɑ ± b |= |b ± ɑ |;
| ɑb |= | ɑ || b |;
| ɑ/b |=| ɑ |/| b |, b ≠0;
|(ɑ+ b) | ≥ | ɑ |-| b |;
|(ɑ+ b) | ≤ | ɑ |+| b |;
|(ɑ- b) | ≥ | ɑ |-| b |;
|(ɑ- b) | ≤ | ɑ |+| b |;
4. Akar Kuadrat
Di dalam matematika, akar kuadrat dari bilangan x sama dengan bilangan r sedemikian sehingga r2 = x, atau, di dalam perkataan lain, bilangan r yang bila dikuadratkan (hasil kali dengan bilangan itu sendiri) sama dengan x. Setiap bilangan real tak-negatif, katakanlah x memiliki akar kuadrat tak-negatif yang tunggal, disebut akar kuadrat utama, yang dilambangkan oleh akar ke-n sebagai√x. Akar kuadrat dapat juga dituliskan dengan notasi eksponen, sebagai x1/2. Misalnya, akar kuadrat utama dari 9 adalah 3, dituliskan dengan √9=3, karena 32 = 3 × 3 = 9 dan 3 tak-negatif. Bagaimanapun, akar kuadrat utama dari sebuah bilangan positif hanya satu dari dua akar kuadratnya.
Setiap bilangan positif x memiliki dua akar kuadrat. Salah satunya adalah √x, yakni yang bernilai positif, sementara yang lainnya adalah -√x, yakni yang bernilai negatif. Kedua-dua akar kuadrat itu dilambangkan dengan ±√x. Akar kuadrat dari bilangan negatif dibahas di dalam kerangka kajian bilangan kompleks. Lebih umum lagi, akar kuadrat dapat dipandang dari beraneka konteks di mana notasi "penguadratan" beberapa objek matematika didefinisi (termasuk aljabar matriks, gelanggang endomorfisma, dll).
Akar kuadrat dari bilangan bulat yang bukan merupakan kuadrat sempurna adalah selalu bilangan irasional (disebut juga bilangan takrasional: bilangan yang tidak dapat dinyatakan sebagai hasil bagi dari dua bilangan bulat. Misalnya, √2 tidak dapat dituliskan secara tepat oleh m/n, di mana n dan m adalah bilangan bulat. Meskipun demikian, ia adalah nilai yang pasti dari panjang diagonal sebuah persegi yang panjang sisinya sama dengan 1. Kejadian ini telah dikenal sejak zaman kuno, dengan ditemukannya bahwa √2 adalah irasional oleh Hippasus, murid dari Pythagoras. (Lihat Akar kuadrat dari 2 untuk membuktikan ketakrasionalan bilangan ini dan irasional kuadrat untuk membuktikan semua bilangan asli yang bukan kuadrat)
Sifat
Fungsi akar kuadrat utama f(x)=√x (biasanya hanya disebut sebagai "fungsi akar kuadrat") adalah fungsi yang memetakan himpunan bilangan real taknegatif R+ ∪ {0} kepada himpunan itu sendiri, dan, seperti
Identitas yang sama dieksploitasi ketika menghitung akar kuadrat dengan tabel logaritma atau slide rule.
Metode iteratif penghitungan akar kuadrat yang paling biasa dilakukan oleh tangan dikenal sebagai "Metode Babilonia" atau "Metode Heron" dinamai demikian untuk menghargai filsuf Yunani Kuno Heron dari Iskandariyah yang pertama memaparkan metode ini. Metode ini melibatkan algoritma sederhana, yang menghasilkan suatu bilangan yang semakin mendekati nilai akar kuadrat sebenarnya tiap kali perulangan dilakukan. Untuk menentukan r, akar kuadrat dari bilangan real x:
5. Sistem koordinat
Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain (sumbu x dan sumbu y), dan panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut (lihat Gambar 1).
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).
Dengan menggunakan sistem koordinat Kartesius, bentuk-bentuk geometri seperti kurva dapat diekspresikan dengan persamaan aljabar. Sebagai contoh, lingkaran yang berjari-jari 2 dapat diekspresikan dengan persamaan x² + y² = 4 (lihat Gambar 2).
Ide dasar sistem ini dikembangkan pada tahun 1637 dalam dua tulisan karya Descartes. Pada bagian kedua dari tulisannya Discourse on Method, ia memperkenalkan ide baru untuk menggambarkan posisi titik atau obyek pada sebuah permukaan, dengan menggunakan dua sumbu yang bertegak lurus antar satu dengan yang lain. Dalam tulisannya yang lain, La Géométrie, ia memperdalam konsep-konsep yang telah dikembangkannya. Lihat koordinat (matematika) untuk sistem-sistem koordinat lain seperti sistem koordinat polar.
Titik pertemuan antara kedua sumbu, titik asal, umumnya diberi label 0. Setiap sumbu juga mempunyai besaran panjang unit, dan setiap panjang tersebut diberi tanda dan ini membentuk semacam grid. Untuk mendeskripsikan suatu titik tertentu dalam sistem koordinat dua dimensi, nilai x ditulis (absis), lalu diikuti dengan nilai y (ordinat). Dengan demikian, format yang dipakai selalu (x,y) dan urutannya tidak dibalik-balik.
Fungsi adalah pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagai kodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10.
Notasi
Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
∈ A ↔ B
Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.
x ∈ A
f : x ↔ x2 atau f(x) = x2
Domain dan Kodomain
Domain adalah daerah asal, kodomain adalah daerah kawan, sedangkan range adalah daerah hasil.
Jenis-Jenis Fungsi
- Fungsi bijektif
Di dalam matematika, akar kuadrat dari bilangan x sama dengan bilangan r sedemikian sehingga r2 = x, atau, di dalam perkataan lain, bilangan r yang bila dikuadratkan (hasil kali dengan bilangan itu sendiri) sama dengan x. Setiap bilangan real tak-negatif, katakanlah x memiliki akar kuadrat tak-negatif yang tunggal, disebut akar kuadrat utama, yang dilambangkan oleh akar ke-n sebagai√x. Akar kuadrat dapat juga dituliskan dengan notasi eksponen, sebagai x1/2. Misalnya, akar kuadrat utama dari 9 adalah 3, dituliskan dengan √9=3, karena 32 = 3 × 3 = 9 dan 3 tak-negatif. Bagaimanapun, akar kuadrat utama dari sebuah bilangan positif hanya satu dari dua akar kuadratnya.
Setiap bilangan positif x memiliki dua akar kuadrat. Salah satunya adalah √x, yakni yang bernilai positif, sementara yang lainnya adalah -√x, yakni yang bernilai negatif. Kedua-dua akar kuadrat itu dilambangkan dengan ±√x. Akar kuadrat dari bilangan negatif dibahas di dalam kerangka kajian bilangan kompleks. Lebih umum lagi, akar kuadrat dapat dipandang dari beraneka konteks di mana notasi "penguadratan" beberapa objek matematika didefinisi (termasuk aljabar matriks, gelanggang endomorfisma, dll).
Akar kuadrat dari bilangan bulat yang bukan merupakan kuadrat sempurna adalah selalu bilangan irasional (disebut juga bilangan takrasional: bilangan yang tidak dapat dinyatakan sebagai hasil bagi dari dua bilangan bulat. Misalnya, √2 tidak dapat dituliskan secara tepat oleh m/n, di mana n dan m adalah bilangan bulat. Meskipun demikian, ia adalah nilai yang pasti dari panjang diagonal sebuah persegi yang panjang sisinya sama dengan 1. Kejadian ini telah dikenal sejak zaman kuno, dengan ditemukannya bahwa √2 adalah irasional oleh Hippasus, murid dari Pythagoras. (Lihat Akar kuadrat dari 2 untuk membuktikan ketakrasionalan bilangan ini dan irasional kuadrat untuk membuktikan semua bilangan asli yang bukan kuadrat)
Sifat
Fungsi akar kuadrat utama f(x)=√x (biasanya hanya disebut sebagai "fungsi akar kuadrat") adalah fungsi yang memetakan himpunan bilangan real taknegatif R+ ∪ {0} kepada himpunan itu sendiri, dan, seperti
 |
| Grafik f(x)=√x, menghasilkan 1/2 parabola dengan irisan kerucut vertikal |
semua fungsi, selalu memiliki nilai balikan yang tunggal. Fungsi akar kuadrat juga memetakan bilangan rasional ke dalam bilangan aljabar (adihimpunan bilangan rasional); √x adalah rasional jika dan hanya jika x adalah bilangan rasional yang dapat dinyatakan sebagai hasil bagi dari dua kuadrat sempurna. Di dalam istilah geometri, fungsi akar kuadrat memetakan luas dari persegi kepada panjang sisinya.
- Untuk setiap bilangan real x
-
- √x2 = | x | = x, jika x ≥ 0= -x, jika x <0
- Untuk setiap bilangan real taknegatif x dan y,
- Fungsi akar kuadrat adalah kontinu untuk setiap bilangan taknegatif x dan terdiferensialkan untuk setiap bilangan positif x. Turunannya diberikan oleh
- Deret Taylor dari √1 + x di dekat x = 0 konvergen ke | x | < 1 dan diberikan oleh
Komputasi
Sebagian besar mesin hitung memiliki tombol akar kuadrat. Lembar kerja komputer dan perangkat lunak lainnya juga seringkali digunakan untuk menghitung akar kuadrat. Program perangkat lunak komputer biasanya menerapkan rutin (perulangan) yang baik untuk menghitung fungsi eksponensial dan logaritma natural atau logaritma, dan kemudian menghitung akar kuadrat dari x menggunakan identitas √x = e1/2 ln x atau √x = 101/2 log x
Metode iteratif penghitungan akar kuadrat yang paling biasa dilakukan oleh tangan dikenal sebagai "Metode Babilonia" atau "Metode Heron" dinamai demikian untuk menghargai filsuf Yunani Kuno Heron dari Iskandariyah yang pertama memaparkan metode ini. Metode ini melibatkan algoritma sederhana, yang menghasilkan suatu bilangan yang semakin mendekati nilai akar kuadrat sebenarnya tiap kali perulangan dilakukan. Untuk menentukan r, akar kuadrat dari bilangan real x:
- Mulakan dengan nilai pemulai positif sembarang r (semakin dekat ke akar kuadrat x, semakin baik).
- Ganti r dengan rata-rata antara r dan x/r, yaitu: (r + x/r)/2 (Adalah cukup untuk mengambil nilai hampiran dari rata-rata itu untuk memastikan konvergensi).
- Ulangi langkah ke-2 hingga r dan x/r cukup dekat dengan nilai yang diharapkan.
5. Sistem koordinat
Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
 |
| Sistem koordinat Kartesius. Terdapat empat titik yang ditandai: (2,3) titik hijau, (-3,1) titik merah, (-1.5,-2.5) titik biru, dan (0,0), titik asal, yang berwarna ungu. |
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).
 |
| Sistem koordinat Kartesius disertai lingkaran merah yang berjari-jari 2 yang berpusat pada titik asal (0,0). Persamaan lingkaran merah ini adalah x² + y² = 4 |
Ide dasar sistem ini dikembangkan pada tahun 1637 dalam dua tulisan karya Descartes. Pada bagian kedua dari tulisannya Discourse on Method, ia memperkenalkan ide baru untuk menggambarkan posisi titik atau obyek pada sebuah permukaan, dengan menggunakan dua sumbu yang bertegak lurus antar satu dengan yang lain. Dalam tulisannya yang lain, La Géométrie, ia memperdalam konsep-konsep yang telah dikembangkannya. Lihat koordinat (matematika) untuk sistem-sistem koordinat lain seperti sistem koordinat polar.
Sistem koordinat dua dimensi
Sistem koordinat Kartesius dalam dua dimensi umumnya didefinisikan dengan dua sumbu yang saling bertegak lurus antar satu dengan yang lain, yang keduanya terletak pada satu bidang (bidang xy). Sumbu horizontal diberi label x, dan sumbu vertikal diberi label y. Pada sistem koordinat tiga dimensi, ditambahkan sumbu yang lain yang sering diberi label z. Sumbu-sumbu tersebut ortogonal antar satu dengan yang lain. (Satu sumbu dengan sumbu lain bertegak lurus.)Titik pertemuan antara kedua sumbu, titik asal, umumnya diberi label 0. Setiap sumbu juga mempunyai besaran panjang unit, dan setiap panjang tersebut diberi tanda dan ini membentuk semacam grid. Untuk mendeskripsikan suatu titik tertentu dalam sistem koordinat dua dimensi, nilai x ditulis (absis), lalu diikuti dengan nilai y (ordinat). Dengan demikian, format yang dipakai selalu (x,y) dan urutannya tidak dibalik-balik.
 |
| Keempat kuadran sistem koordinat Kartesius. Panah yang ada pada sumbu berarti panjang sumbunya tak terhingga pada arah panah tersebut. |
Pilihan huruf-huruf didasari oleh konvensi, yaitu huruf-huruf yang dekat akhir (seperti x dan y) digunakan untuk menandakan variabel dengan nilai yang tak diketahui, sedangkan huruf-huruf yang lebih dekat awal digunakan untuk menandakan nilai yang diketahui. Karena kedua sumbu bertegak lurus satu sama lain, bidang xy terbagi menjadi empat bagian yang disebut kuadran, yang pada Gambar 3 ditandai dengan angka I, II, III, dan IV. Menurut konvensi yang berlaku, keempat kuadran diurutkan mulai dari yang kanan atas (kuadran I), melingkar melawan arah jarum jam (lihat Gambar 3). Pada kuadran I, kedua koordinat (x dan y) bernilai positif. Pada kuadran II, koordinat x bernilai negatif dan koordinat y bernilai positif. Pada kuadran III, kedua koordinat bernilai negatif, dan pada kuadran IV, koordinat x bernilai positif dan y negatif (lihat tabel dibawah ini).
| ||||||||||||||||||
Fungsi dan Limit
Fungsi
Fungsi adalah pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagai kodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10.
Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
∈ A ↔ B
Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.
x ∈ A
f : x ↔ x2 atau f(x) = x2
Fungsi sebagai Relasi
Sebuah fungsi f dapat dimengerti sebagai relasi antara dua himpunan, dengan unsur pertama hanya dipakai sekali dalam relasi tersebut.Domain dan Kodomain
Domain adalah daerah asal, kodomain adalah daerah kawan, sedangkan range adalah daerah hasil.
Jenis-Jenis Fungsi
- Fungsi injektif
Fungsi f: A → B disebut fungsi satu-satu atau fungsi injektif jika dan hanya jika untuk sebarang a1 dan a2 ∈A dengan a1 tidak sama dengan a2 berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).- Fungsi surjektif
Fungsi f: A → B disebut fungsi kepada atau fungsi surjektif jika dan hanya jika untuk sebarang b dalam kodomain B terdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range).- Fungsi bijektif
Fungsi f: A → B disebut disebut fungsi bijektif jika dan hanya jika untuk sebarang b dalam kodomain B terdapat tepat satu a dalam domain A sehingga f(a) = b, dan tidak ada anggota A yang tidak terpetakan dalam B. Dengan kata lain, fungsi bijektif adalah sekaligus injektif dan surjektif.
Trigonometri
Trigonometri adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometri seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanika, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan "penyebaran" dan "quadrance", bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales. Informasi lebih lanjut bisa dilihat di situs webnya.
Hubungan fungsi trigonometri
sin2A + cos2A = 1
1+tan2A = 1/cos2A = sec2A
1+cot2A = csc2A tan A = sin A/cos A
Penjumlahan
sin (A+B) = sin A cos B + cos A sin B
sin (A-B) = sin A cos B - cos A sin B
cos (A+B) = cos A cos B - sin A sin B
cos (A-B) = cos A cos B + sin A sin B
tan (A+B) = tan A + tan B / 1 - tan A tan B
tan (A-B) = tan A - tan B / 1 + tan A tan B
Trigonometri
Trigonometri adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometri seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanika, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan "penyebaran" dan "quadrance", bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales. Informasi lebih lanjut bisa dilihat di situs webnya.
Hubungan fungsi trigonometri
sin2A + cos2A = 1
1+tan2A = 1/cos2A = sec2A
1+cot2A = csc2A tan A = sin A/cos A
Penjumlahan
sin (A+B) = sin A cos B + cos A sin B
sin (A-B) = sin A cos B - cos A sin B
cos (A+B) = cos A cos B - sin A sin B
cos (A-B) = cos A cos B + sin A sin B
tan (A+B) = tan A + tan B / 1 - tan A tan B
tan (A-B) = tan A - tan B / 1 + tan A tan B
Rumus sudut rangkap dua
cos 2A = cos2A - sin2A = 2 cos2A - 1 = 1 - 2sin2A
tan 2A = 2 tanA / 1 - tan2A = 2 cot A / cot2A - 1 = 2 / cot A - tan A
Rumus sudut rangkap tiga
sin 3 A = 3 sin A - 4 sin3 A
cos 3A = 4 cos3 A- 3 cos A
Rumus setengah sudut
sin A/2 = ± √1 - cos A / 2
cos A/2 = ± √1 + cos A / 2
tan A/2 = ± √1 - cos A / 1 + cos A / 2 = sin A / 1 + cos A = 1 - cos A / sin A
dimana f '(x) = lim h→0 f (x + h) - f(x) / h
maka turunan fungsi trigonometri akan mempunyai rumus :
f(x) = sin x maka f '(x) = cos x
f(x) = cos x maka f '(x) = - sin x
f(x) = a.sin (bx + c) maka f '(x) = ab.cos (bx +c)
f(x) = a.cos (bx + c) maka f '(x) = - ab.sin (bx +c)
Dalam pelajaran matematika, limit biasanya mulai dipelajari saat pengenalan terhadap kalkulus, dan untuk memahami konsep limit secara menyeluruh bukan sesuatu yang mudah.
 R terdefinisi pada garis bilangan riil, dan p, L
R terdefinisi pada garis bilangan riil, dan p, L  R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:
R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:
jika dan hanya jika untuk setiap ε > 0 terdapat δ > 0 sehingga |x - p|< δ mengimplikasikan bahwa |f (x) - L | < ε . Di sini, baik ε maupun δ merupakan bilangan riil. Perhatikan bahwa nilai limit tidak tergantung pada nilai f (p)
limx→p+ f (x) = L
Definisi formal adalah sebagai berikut. Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) - L| < ε pada saat 0 < x - p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) - L| < ε bilamana 0 < p - x < δ.
Bila limitnya tidak ada terdapat osilasi matematis tidak nol.
Bila f(x) adalah fungsi riil, maka limit f saat x mendekati tak hingga adalah L, dilambangkan sebagai:
Dengan cara yang sama, limit f saat x mendekati tak hingga adalah tak hingga, dilambangkan oleh
limx→∞ f (x) = ∞
jika dan hanya jika bila untuk semua R > 0 terdapat S > sedemikian sehingga f(x) > R bilamana x > S.
Untuk lebih cermat, kita mengatakan bahwa fungsi f kontinu pada suatu titik c bila dua persyaratan berikut terpenuhi:
Perhatikan suatu fungsi f yang memetakan himpunan bilangan riil kepada himpunan bilangan riil lainnya, dan misalkan c adalah termasuk dalam domain f. Fungsi f dikatakan kontinu pada titik c bila pernyataan berikut berlaku: Untuk tiap bilangan ε > 0, seberapa pun kecilnya, terdapat suatu bilangan δ > 0 sedemikian sehingga untuk semua x dalam domain dengan c - δ < x < c + δ, nilai f(x) memenuhi:
f (c) - ԑ < f (x) < f (c) + ԑ
|x-c| < δ → |f (x) - f (c)| < ԑ
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
f' (x) = limh→0 f (x+h) - f (x) / h
Apabila z = x + h, h = x - z, dan h mendekati 0 jika dan hanya jika z mendekati x, maka definisi turunan di atas dapat pula kita tulis sebagai:
f' (x) = limz→x f (z) - f (x) / z - x
Perhatikan bahwa ekspresi f (x + h) - f (x) / h pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
Sebagai contoh, untuk menemukan gradien dari fungsi f(x) = x2 pada titik (3,9):
f ' (3) = limh→0 (3 + h)2 - 9 / h
Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
dy/dx, df/dx.(x), ataupun d/dx. f(x)
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila y = ƒ(t), maka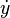 mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk memberikan turunan pertamanya Df. Apabila y = ƒ(x) adalah variabel terikat, maka sering kali x dilekatkan pada D untuk mengklarifikasikan keterbebasan variabel x. Notasi Euler kemudian ditulis sebagai:
Dxy atau Dxf (x)
Kaidah penurunan umum
(cf)' = cf'
(f + g)' = f' + g'
(fg)' = f'g + fg'
(1/f)' = -f'/ f2 , f ≠ 0
(f/g)' = f'g = fg' / g2 , g ≠ 0
d/dx [ln (f(x))] = f'(x) / f (x)
d/dx logb (x) = d/dx . ln(x)/ln(b) = 1/x ln(b) logb (e) / x
Turunan fungsi hiperbolik
(sin h x)' = cos h x = ex + e-x/2 (arc sin h x)' = 1/√x2+1
(cos h x)' = sin h x = ex - e-x/2 (arc cos h x)' = 1/√x2-1
(tan h x)' = sec h2 x (arc tan h x)' = 1/ 1 - x2
(sec h x)' = - tan h x sec h x (arc sec h x)' = -1/x √1-x2
(csc h x)' = - cot h x csc h x (arc csc h x)' = -1/x √1+x2
(cot h x)' = - csc h2 x (arc cot h x)' = -1/x2 -1
(Г(x))' = ∫(0-∞)tx-1e-t ln t dt
(Г(x))' = Г(x) (∑ (n=1 - ∞(ln(1 + 1/n) - 1 / x+n) - 1/x) = Г(x) ψ (x)
Aturan rantai
Dalam kalkulus, kaidah rantai atau aturan rantai adalah rumus untuk turunan fungsi komposit (fungsi bersusun) dari dua fungsi matematika. Secara intuitif, bila variabel y bergantung pada variabel kedua, u, yang pada gilirannya bergantung pada variabel ketiga, x, maka laju perubahan y terhadap x dapat dihitung sebagai laju perubahan y terhadap u dikalikan dengan laju perubahan u terhadap x. Ini dapat dituliskan sebagai
dy/dx = dy/du. du/dx
Dalam kalkulus, notasi Leibniz menggunakan simbol dx dan dy untuk melambangkan pertambahan "kecil takhingga" (atau infinitesimal) dari x dan y, sebagaimana Δx dan Δy melambangkan pertambahan hingga dari x dan y. Untuk y sebagai fungsi dari x
y = f(x),
dy/dx = f'(x) ,
Meskipun sekarang matematikawan memandang integral
∫ f (x) dx
lim∆x→0 ∑i f (xi) ∆x
dengan Δx adalah selang yang mengandung xi, Leibniz memandangnya sebagai jumlahan (lambang integral menandakan penjumlahan) kuantitas infinitesimal yang banyaknya takhingga f(x) dx.
Salah satu kelebihan sudut pandang Leibniz adalah kesesuaiannya dengan analisis dimensi. Sebagai contoh, dalam notasi Leibniz, turunan kedua (menggunakan penurunan implisit) adalah
d2 y / dx2 = f '' (x)
Rumus setengah sudut
sin A/2 = ± √1 - cos A / 2
cos A/2 = ± √1 + cos A / 2
tan A/2 = ± √1 - cos A / 1 + cos A / 2 = sin A / 1 + cos A = 1 - cos A / sin A
turunan fungsi trigonometri
Untuk menentukan turunan trigonometri sama dengan konsep awal mencari turunan, namun disini langsung kita ambil hasilnya.dimana f '(x) = lim h→0 f (x + h) - f(x) / h
maka turunan fungsi trigonometri akan mempunyai rumus :
f(x) = sin x maka f '(x) = cos x
f(x) = cos x maka f '(x) = - sin x
f(x) = a.sin (bx + c) maka f '(x) = ab.cos (bx +c)
f(x) = a.cos (bx + c) maka f '(x) = - ab.sin (bx +c)
Limit
Konsep limit digunakan untuk menjelaskan sifat dari suatu fungsi, saat argumen mendekati ke suatu titik, atau tak hingga; atau sifat dari suatu barisan saat indeks mendekati tak hingga. Limit dipakai dalam kalkulus (dan cabang lainnya dari analisis matematika) untuk mencari turunan dan kekontinuan. |
| Definisi limit: kita katakan bahwa limit f(x) ketika x mendekati titik p adalah L apabila untuk setiap bilangan ε > 0 apapun, terdapat bilangan δ > 0, sedemikian rupanya: 0 < | x - p | < δ → | f (x) - L | < ∈ |
Fungsi pada garis bilangan riil
Bila f : R R terdefinisi pada garis bilangan riil, dan p, L
R terdefinisi pada garis bilangan riil, dan p, L  R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:
R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:limx→p f (x) = L
jika dan hanya jika untuk setiap ε > 0 terdapat δ > 0 sehingga |x - p|< δ mengimplikasikan bahwa |f (x) - L | < ε . Di sini, baik ε maupun δ merupakan bilangan riil. Perhatikan bahwa nilai limit tidak tergantung pada nilai f (p)
Limit searah
Masukan x dapat mendekati p dari atas (kanan di garis bilangan) atau dari bawah (kiri). Dalam hal ini limit masing-masingnya dapat ditulis sebagailimx→p+ f (x) = L
- atau limx→p- f (x) = L
Definisi formal adalah sebagai berikut. Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) - L| < ε pada saat 0 < x - p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) - L| < ε bilamana 0 < p - x < δ.
Bila limitnya tidak ada terdapat osilasi matematis tidak nol.
Limit fungsi pada ketakhinggaan
Bila dua unsur, ketakhinggaan positif dan negatif {-∞, +∞}, ditambahkan pada garis bilangan riil, kita dapat mendefinisikan limit fungsi pada ketakhinggaan. Dua unsur tambahan ini bukanlah bilangan, namun berguna dalam memerikan kelakuan limit pada kalkulus dan analisis.Bila f(x) adalah fungsi riil, maka limit f saat x mendekati tak hingga adalah L, dilambangkan sebagai:
limx→∞ f (x) = L
Dengan cara yang sama, limit f saat x mendekati tak hingga adalah tak hingga, dilambangkan oleh
limx→∞ f (x) = ∞
jika dan hanya jika bila untuk semua R > 0 terdapat S > sedemikian sehingga f(x) > R bilamana x > S.
Fungsi kontinu
Fungsi kontinu dalam matematika adalah fungsi, yang bila dijelaskan secara intuitif, perubahan kecil dalam masukannya berakibat perubahan kecil pula pada keluaran. Bila tidak demikian, fungsi tersebut dikatakan diskontinu. Fungsi kontinu dengan fungsi invers kontinu pula disebut bikontinu. Gagasan intuitif kekontinuan dapat diberikan oleh pernyataan bahwa fungsi kontinu adalah fungsi yang grafiknya dapat digambar tanpa mengangkat kapur dari papan tulis. Kekontinuan fungsi merupakan salah satu konsep inti topologi. Sebagai contoh fungsi kontinu, perhatikan fungsi h(t), yang memerikan tinggi bunga yang sedang tumbuh pada waktu t. Fungsi ini kontinu. Terdapat diktum dalam fisika klasik yang menyatakan bahwa di alam semuanya kontinu. Sebaliknya, jika M(t) melambangkan jumlah uang di sebuah rekening bank pada waktu t, fungsi ini melompat ketika uang disimpan atau ditarik. Karena itu fungsi M(t) diskontinu.Fungsi riil kontinu
Misalkan kita memiliki fungsi yang memetakan bilangan riil kepada bilangan riil, dengan domainnya merupakan suatu selang, seperti fungsi h dan M di atas. Fungsi seperti ini dapat dilambangkan dengan grafik dalam bidang Cartesius. Secara kasar dapat dikatakan fungsi tersebut kontinu bila grafik itu berupa kurva tunggal tidak terputus, tanpa "lubang" atau "lompatan"Untuk lebih cermat, kita mengatakan bahwa fungsi f kontinu pada suatu titik c bila dua persyaratan berikut terpenuhi:
- f(c) harus terdefinisi (c termasuk dalam domain f)
- limit f(x) saat x mendekati c baik dari kiri maupun dari kanan ada, dan harus sama dengan f(c).
Definisi Cauchy untuk fungsi kontinu
Tanpa harus menggunakan konsep limit, kita dapat mendefinisikan kekontinuan fungsi riil sebagai berikut:Perhatikan suatu fungsi f yang memetakan himpunan bilangan riil kepada himpunan bilangan riil lainnya, dan misalkan c adalah termasuk dalam domain f. Fungsi f dikatakan kontinu pada titik c bila pernyataan berikut berlaku: Untuk tiap bilangan ε > 0, seberapa pun kecilnya, terdapat suatu bilangan δ > 0 sedemikian sehingga untuk semua x dalam domain dengan c - δ < x < c + δ, nilai f(x) memenuhi:
f (c) - ԑ < f (x) < f (c) + ԑ
|x-c| < δ → |f (x) - f (c)| < ԑ
Diferensiasi
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
f' (x) = limh→0 f (x+h) - f (x) / h
Apabila z = x + h, h = x - z, dan h mendekati 0 jika dan hanya jika z mendekati x, maka definisi turunan di atas dapat pula kita tulis sebagai:
f' (x) = limz→x f (z) - f (x) / z - x
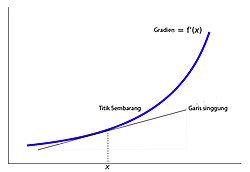 |
| Garis singgung pada (x, f(x)). Turunan f'(x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. |
Sebagai contoh, untuk menemukan gradien dari fungsi f(x) = x2 pada titik (3,9):
f ' (3) = limh→0 (3 + h)2 - 9 / h
= limh→0 9 + 6h + h2 - 9 / h
= limh→0 6h + h2 / h
= limh→0 (6 + h)
= 6
Notasi pendiferensialan
Terdapat berbagai macam notasi matematika yang dapat digunakan digunakan untuk menyatakan turunan, meliputi notasi Leibniz, notasi Lagrange, notasi Newton, dan notasi Euler.Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
dy/dx, df/dx.(x), ataupun d/dx. f(x)
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila y = ƒ(t), maka
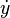 mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk memberikan turunan pertamanya Df. Apabila y = ƒ(x) adalah variabel terikat, maka sering kali x dilekatkan pada D untuk mengklarifikasikan keterbebasan variabel x. Notasi Euler kemudian ditulis sebagai:
Dxy atau Dxf (x)
| Notasi Leibniz | Notasi Lagrange | Notasi Newton | Notasi Euler | |
|---|---|---|---|---|
| Turunan ƒ(x) terhadap x | d/dx.f(x) | ƒ′(x) | ẏ dengan y = ƒ(x) | Dxf(x) |
Aturan menentukan turunan fungsi
Turunan dasar
Aturan - aturan dalam turunan fungsi adalah:- f(x), maka f'(x) = 0
- Jika f(x) = x, maka f’(x) = 1
- Aturan pangkat : Jika f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta : (kf) (x) = k. f’(x)
- Aturan rantai : ( f o g ) (x) = f’ (g (x)). g’(x))
Turunan jumlah, selisih, hasil kali, dan hasil bagi dua fungsi
Misalkan fungsi f dan g terdiferensialkan pada selang I, maka fungsi f + g, f – g, fg, f/g, ( g (x) ≠ 0 pada I ) terdiferensialkan pada I dengan aturan:- ( f + g )’ (x) = f’ (x) + g’ (x)
- ( f – g )’ (x) = f’ (x) + g’ (x)
- (fg)’ (x) = f (x) g’(x) + g’(x) f(x)
- ((f)/g )’ (x) = (g(x) f' (x)- f(x) g' (x))/((g(x)2)
Turunan fungsi trigonometri
- d/dx ( sin x ) = cos x
- d/dx ( cos x ) = - sin x
- d/dx ( tan x ) = - sec2 x
- d/dx ( cot x ) = - csc2 x
- d/dx ( sec x ) = sec x tan x
- d/dx ( csc x ) = -csc x cot x
Turunan fungsi invers
(f-1)(y) = 1/(f' (x)), atau dy/dx = 1/(dx/dy)
Kaidah penurunan umum
(cf)' = cf'
(f + g)' = f' + g'
(fg)' = f'g + fg'
(1/f)' = -f'/ f2 , f ≠ 0
(f/g)' = f'g = fg' / g2 , g ≠ 0
- Kaidah rantai
- (f ○ g) = (f' ○ g) g'
- Turunan fungsi invers
- f -1 )' = 1/f' ○ f -1
- Kaidah pangkat umum
- (f g)' = f g (g' ln f + g/f. f ')
- Turunan fungsi sederhana
- c' = 0
- x' = 1
- (cx') = c
- | x |' = x / | x | = sgn x, x ≠ 0
- ( xc)' = cxc-1 baik xc maupun cxc-1 terdefinisi
- (1/x)' = (x-1)' = -x-2 = -1/x2
- (1/xc)' = (x-c)' = -cx-(c+1) = - c / xc+1
- (√x)' = (x1/2)' = 1/2 x-1/2 = 1/2√x' x >0
- Turunan fungsi eksponensial dan logaritmik
- (cx)' = cx ln c, c>0
- Perhatikan bahwa persamaan tersebut berlaku untuk semua c, namun turunan tersebut menghasilkan bilangan kompleks
- (ex)' = ex
- (logc x)' = 1/x ln c , c > 0, c ≠ 1
- Persamaan di atas juga berlaku untuk semua c namun menghasilkan bilangan kompleks
- (ln x)' = 1/x , x ≠ 0
- (ln | x |)' = 1/x
- (xx)' = xx (1 + ln x)
d/dx [ln (f(x))] = f'(x) / f (x)
d/dx logb (x) = d/dx . ln(x)/ln(b) = 1/x ln(b) logb (e) / x
Turunan fungsi trigonometri
(sin x)' = cos x (arc sin x)' = 1 / √1 - x2
(cos x)' = - sin x (arc cos x)' = -1 / √1 - x2
(tan x)' = sec2 x = 1/ cos2 x (arc tan x)' = 1/1 + x2
(sec x)' = sec x tan x (arc sec x)' = 1/ | x | √x2-1
(csc x)' = - csc x cot x (arc csc x)' = -1/ | x | √x2-1
(cot x)' = - csc2 x = -1 / sin2 x (arc cot x)' = -1 / 1 + x2Turunan fungsi hiperbolik
(sin h x)' = cos h x = ex + e-x/2 (arc sin h x)' = 1/√x2+1
(cos h x)' = sin h x = ex - e-x/2 (arc cos h x)' = 1/√x2-1
(tan h x)' = sec h2 x (arc tan h x)' = 1/ 1 - x2
(sec h x)' = - tan h x sec h x (arc sec h x)' = -1/x √1-x2
(csc h x)' = - cot h x csc h x (arc csc h x)' = -1/x √1+x2
(cot h x)' = - csc h2 x (arc cot h x)' = -1/x2 -1
- Turunan fungsi khusus
Fungsi gamma
(Г(x))' = ∫(0-∞)tx-1e-t ln t dt
(Г(x))' = Г(x) (∑ (n=1 - ∞(ln(1 + 1/n) - 1 / x+n) - 1/x) = Г(x) ψ (x)
- Fungsi Riemann Zeta
- (ϛ(x))' = -∑ (n=1 - ∞) ln n / nx = - ln 2 / 2x - ln 3 / 3x - ln 4 / 4x - ...
(ϛ(x))' = -∑ p prime p-x ln p / (1- p-x)2 ∏ q prime, q≠p 1 / 1 - q-x
Aturan rantai
Dalam kalkulus, kaidah rantai atau aturan rantai adalah rumus untuk turunan fungsi komposit (fungsi bersusun) dari dua fungsi matematika. Secara intuitif, bila variabel y bergantung pada variabel kedua, u, yang pada gilirannya bergantung pada variabel ketiga, x, maka laju perubahan y terhadap x dapat dihitung sebagai laju perubahan y terhadap u dikalikan dengan laju perubahan u terhadap x. Ini dapat dituliskan sebagai
dy/dx = dy/du. du/dx
Notasi Leibniz
Dalam kalkulus, notasi Leibniz menggunakan simbol dx dan dy untuk melambangkan pertambahan "kecil takhingga" (atau infinitesimal) dari x dan y, sebagaimana Δx dan Δy melambangkan pertambahan hingga dari x dan y. Untuk y sebagai fungsi dari x
y = f(x),
lim∆x→0 ∆y/∆x = lim∆x→0 f (x + ∆x) - f(x) / ∆x,
adalah, menurut Leibniz, hasil bagi dari pertambahan kecil takhingga dari y oleh pertambahan kecil takhingga x, atau
dy/dx = f'(x) ,
Meskipun sekarang matematikawan memandang integral
∫ f (x) dx
lim∆x→0 ∑i f (xi) ∆x
dengan Δx adalah selang yang mengandung xi, Leibniz memandangnya sebagai jumlahan (lambang integral menandakan penjumlahan) kuantitas infinitesimal yang banyaknya takhingga f(x) dx.
Salah satu kelebihan sudut pandang Leibniz adalah kesesuaiannya dengan analisis dimensi. Sebagai contoh, dalam notasi Leibniz, turunan kedua (menggunakan penurunan implisit) adalah
d2 y / dx2 = f '' (x)





